Comparison of images for different models
At low frequencies no ageing has taken place, so there are no
differences between the models. The differences in the high frequency
images are due to differential ageing of the points in the emitting
region. Although this was described for the individual models, I cover
it again here for all the models together.
If inverse Compton losses dominate, or if diffusion is efficient so
that the current local field is not the dominant contributor to an
electron's total energy losses, then the break energy and electron
energy spectrum are the same everywhere. Because the magnetic field
varies, the break frequency, proportional to the field strength, varies
from place to place. In this case the ageing appears most rapid in the
low field regions because they have the lowest break frequencies.
As the importance of local losses increases, spatial variations in the
break energy and energy spectrum become more pronounced. Electrons in
the stronger field regions have above average losses and the break
energy is correspondingly reduced. There are now two competing effects.
For a given break energy, increasing the field strength increases the
break frequency. This is the same in all the models. But as the
importance of local losses increases (as the inverse Compton and
diffusive effects decrease), the break energy is lower in the stronger
field regions. For very strong fields, corresponding to weak inverse
Compton losses or little diffusion, the spatial variations in the break
energy are dominant. At the other extreme, the spatial variations in
break energy are unimportant. There is an intermediate regime, where
the spatial variations in break frequency is minimized.
The histograms of pixel intensity (Figures 2, 4, & 6) at high frequency
differ substantially between the models. In the low field, high
diffusion model a long tail containing a few bright points appears.
These are the last few points that have not yet aged. The histograms at
high frequency for the other two cases appear rather similar - in both
cases a tail of bright points is just starting to appear. There are
differences, however. In the intermediate case there is little
intrinsic difference in intensity, as the break frequency is reasonably
independent of local conditions. These small differences are then
exaggerated by the steep spectral index in this model. For the high
field, low diffusion model the spectral index at high frequencies is
much flatter and the evolution of the intensity histogram is driven by
the strong dependence of break frequency on local conditions.
While there is not a great deal of difference between the
high-frequency images for the intermediate- and high-field strength
cases, the ageing will be much easier to observe in the high field
strength case. This is because the shape of the spectrum (as discussed
in the next section) is different - the overall intensity of the
intermediate field strength image falls much more rapidly, so that
sources with  >>
>> 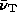 will be very faint and almost undetectable, while the
high field, low diffusion sources will be much easier to observe. In
addition,
will be very faint and almost undetectable, while the
high field, low diffusion sources will be much easier to observe. In
addition, 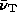 is much lower in the high field case,
so that at a fixed time the frequency will be higher relative to the
break than in the other models. The combination of these effects means
that the high frequency behaviour of the high field models is most
relevant to observations.
is much lower in the high field case,
so that at a fixed time the frequency will be higher relative to the
break than in the other models. The combination of these effects means
that the high frequency behaviour of the high field models is most
relevant to observations.
___________________________________
Peter Tribble, peter.tribble@gmail.com
 >>
>> 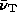 will be very faint and almost undetectable, while the
high field, low diffusion sources will be much easier to observe. In
addition,
will be very faint and almost undetectable, while the
high field, low diffusion sources will be much easier to observe. In
addition, 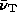 is much lower in the high field case,
so that at a fixed time the frequency will be higher relative to the
break than in the other models. The combination of these effects means
that the high frequency behaviour of the high field models is most
relevant to observations.
is much lower in the high field case,
so that at a fixed time the frequency will be higher relative to the
break than in the other models. The combination of these effects means
that the high frequency behaviour of the high field models is most
relevant to observations.