 > 10
> 10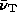 where the very faintest regions start to have
steeper spectra.
where the very faintest regions start to have
steeper spectra.There are two aspects of the filaments that any model should explain. These are the shape of the filaments and their enhanced brightness relative to the background emission. The models presented in this paper do not reproduce the linear structures often seen because I have assumed the magnetic field to be a Gaussian random field. The important point to note is that enhanced contrast can and will be obtained from a nonuniform field together with spectral ageing. At low frequencies the image is relatively smooth, with fluctuations about a mean level. At high frequencies the correct description is of high peaks on a generally low background, and it is these local peaks that I am referring to as `filaments.' It is not necessary to invoke instabilities to explain high contrast emission, although a more detailed model of the field structure is necessary to explain the shapes of the filaments.
The effect of spectral ageing in making a source appear more filamentary at high frequencies is perfectly general and does not depend on the assumption of a Gaussian random field. Any intensity histogram will develop a tail of bright points which have not yet faded as the electron population ages.
One way to differentiate between various models for filament formation
is to examine the spectral indices of the filament and inter-filament
emission (Hines et al. 1989; Carilli et al. 1991). I have considered
this in Section 4, with some examples in Fig.
8. In the low-field (high diffusion) case, the inter-filament regions
have steeper spectra than the bright peaks. This is true at all
frequencies, although at low frequencies the difference in spectral
indices is very small. In the intermediate case the correlation between
intensity and spectral index is weak, except at very high frequencies
 > 10
> 10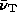 where the very faintest regions start to have
steeper spectra.
where the very faintest regions start to have
steeper spectra.
In the high field case, for low frequencies  < 0.1
< 0.1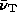 the bright regions have steeper spectra, whereas at
high frequencies the situation is reversed so that the brighter regions
tend to have flatter spectra. This behaviour arises because the
initially bright regions fade and steepen most rapidly. At low
frequencies they are still the brightest regions, so the brighter
regions have steeper spectra. At high frequencies the initially bright
regions have faded, so the bright regions are now unaged regions of low
field and have flatter spectra.
the bright regions have steeper spectra, whereas at
high frequencies the situation is reversed so that the brighter regions
tend to have flatter spectra. This behaviour arises because the
initially bright regions fade and steepen most rapidly. At low
frequencies they are still the brightest regions, so the brighter
regions have steeper spectra. At high frequencies the initially bright
regions have faded, so the bright regions are now unaged regions of low
field and have flatter spectra.
In the low-field, high-diffusion case the correlation between intensity and spectral index is tight. The intermediate- and high-field cases show a great deal of scatter about the mean relation, so that an individual filament may not be typical of the source as a whole.
Explaining radio filaments by synchrotron ageing therefore has several advantages. Synchrotron ageing is ubiquitous and does not require special conditions in the source. The timescale for filament formation is the ageing timescale itself. And, at high frequency, the filaments will be bright and have a flatter spectral index than their surroundings, because the spectra steepen as they age, and the observed filaments are the least aged regions. For the low-field case, the filaments have flatter spectra at all frequencies.
On to:
Up to: ___________________________________ Peter Tribble, peter.tribble@gmail.com