Model uncertainties
There is little room for uncertainty in the calculation of the
accumulated magnetic energy density in radio source remnants. The
result is insensitive to the choice of lower luminosity limit and
maximum redshift, as discussed in Section
5.1. The radio luminosity function is well known in the region of
interest. The major uncertainties are the equipartition assumption, the
assumption that the all the energy is turned into radio luminosity, and
the assumption that all sources are included in the integral.
The derived energy density will be in error by whatever factor the
equipartition estimate is, and it is difficult to assess how large this
uncertainty is likely to be. This problem will afflict any calculation
of the magnetic energy content of radio sources - it is not peculiar to
the model presented in this paper.
Another uncertainty is the assumption that all of the original energy
in relativistic electrons is radiated in observable radio emission and
is included in the integral over the luminosity function. Van der Laan
& Perola (1969) argued that the lack of a large population of steep
spectrum sources meant that sources must die quickly rather than simply
fade away by radiative or adiabatic losses, and suggested a model where
the relativistic electrons were lost by diffusion out of the source.
The sources also lose energy by inverse Compton scattering. In both
cases the estimate of the energy density I have given must be revised
upwards to allow for the fraction of the particle energy that is lost
to inverse Compton radiation, and the fraction of energy lost by
particles leaving the source and no longer contributing to the observed
luminosity.
The magnetic energy density could be underestimated by a factor of a
few in this way. While very luminous sources have field strengths
greater than the inverse Compton equivalent of 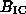 = 3.18(1+z)^2
= 3.18(1+z)^2 ,
, 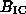 increases from 12 to 50
increases from 12 to 50 in the
redshift range of interest (z=1--3), so that the intermediate
luminosity sources which dominate the integral
in the
redshift range of interest (z=1--3), so that the intermediate
luminosity sources which dominate the integral 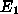 (see Fig. 1) lose a substantial fraction of their energy
to inverse Compton radiation. This effect is even more important if
the magnetic field strength is lower than the equipartition estimate.
Lowering the magnetic field strength of a source reduces its
contribution to the magnetic energy density, but this is compensated
for by the fact that the energy density is underestimated because a
smaller fraction of the total energy is emitted in the radio waveband
and thus included in the integral over source luminosity. As a result,
the actual energy density could be substantially higher than the energy
density I have derived, but is unlikely to be substantially less.
(see Fig. 1) lose a substantial fraction of their energy
to inverse Compton radiation. This effect is even more important if
the magnetic field strength is lower than the equipartition estimate.
Lowering the magnetic field strength of a source reduces its
contribution to the magnetic energy density, but this is compensated
for by the fact that the energy density is underestimated because a
smaller fraction of the total energy is emitted in the radio waveband
and thus included in the integral over source luminosity. As a result,
the actual energy density could be substantially higher than the energy
density I have derived, but is unlikely to be substantially less.
The energy density could also be underestimated due to a new population
of low luminosity sources. As discussed in Section 5.1, the derived energy density does not
rely on extrapolation of the luminosity function to low luminosities.
Therefore, changing the luminosity function cannot decrease the energy
density. It is always possible that a new population of sources could
lead to a substantial upturn in the luminosity function at low
luminosities and increase the energy density somewhat. I will briefly
mention two possible classes of object that might be present at low
luminosities.
The interstellar medium of cluster galaxies could be stripped and mixed
into the intracluster medium. While little is known about magnetic
fields in elliptical galaxies, the interstellar medium in spiral
galaxies contains magnetic fields of  strength
(Wielebinski & Krause 1993). As the galaxy passes through the
intracluster medium the interstellar medium is stripped by ram
pressure, depositing enriched gas and magnetic fields into the cluster
gas. If a spiral galaxy has a 3
strength
(Wielebinski & Krause 1993). As the galaxy passes through the
intracluster medium the interstellar medium is stripped by ram
pressure, depositing enriched gas and magnetic fields into the cluster
gas. If a spiral galaxy has a 3 field in a
volume of 1000 kpc^3 then the magnetic energy is ~10^48 J. A thousand
such galaxies gives a total of 10^51 J. While this is a very
substantial energy content, it is only a very small fraction of the
energy input by powerful radio sources.
field in a
volume of 1000 kpc^3 then the magnetic energy is ~10^48 J. A thousand
such galaxies gives a total of 10^51 J. While this is a very
substantial energy content, it is only a very small fraction of the
energy input by powerful radio sources.
Another possible class of radio sources which might not have been
included are the giant or relic sources. An example is 0917+75, which
has been considered by Harris et al. (1993). Harris et al. show that this
relic, of relatively low luminosity, has a similar energy content to
the Coma radio halo, so that this source alone has sufficient magnetic
energy to magnetize a significant fraction of a cluster. Due to the low
field strength, these giant sources are of low luminosity. Due to their
low surface brightness, they might be missed in interferometric
surveys.
While both the stripped interstellar media of galaxies and giant radio
sources can clearly contribute to an intracluster magnetic field, it is
clear that their contribution is small compared to that of powerful
radio galaxies, and that their is in fact no shortage of magnetic
energy. Even if the equipartition estimate is in error, this does not
affect the fundamental conclusion that powerful radio sources can give
 strength
fields in clusters at the present time. The estimate of accumulated
magnetic energy would have to be reduced by more than an order of
magnitude before it would have any problem giving the observed
fields.
strength
fields in clusters at the present time. The estimate of accumulated
magnetic energy would have to be reduced by more than an order of
magnitude before it would have any problem giving the observed
fields.
The results are also insensitive to the choice of cosmological model.
Changing the Hubble constant H_0 changes the space density 
 H_0^3, the
real luminosity L
H_0^3, the
real luminosity L  H_0^-2 and the age of the universe
t_0
H_0^-2 and the age of the universe
t_0  H_0^-1, leading to an energy density independent of H_0. The energy per
cluster is likewise independent of H_0 as, while the space density of
clusters changes, so does the physical size of each cluster. Therefore
the derived magnetic field strengths are independent of H_0.
H_0^-1, leading to an energy density independent of H_0. The energy per
cluster is likewise independent of H_0 as, while the space density of
clusters changes, so does the physical size of each cluster. Therefore
the derived magnetic field strengths are independent of H_0.
Peter Tribble, peter.tribble@gmail.com
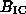 = 3.18(1+z)^2
= 3.18(1+z)^2 ,
, 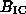 increases from 12 to 50
increases from 12 to 50 in the
redshift range of interest (z=1--3), so that the intermediate
luminosity sources which dominate the integral
in the
redshift range of interest (z=1--3), so that the intermediate
luminosity sources which dominate the integral 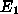 (see Fig. 1) lose a substantial fraction of their energy
to inverse Compton radiation. This effect is even more important if
the magnetic field strength is lower than the equipartition estimate.
Lowering the magnetic field strength of a source reduces its
contribution to the magnetic energy density, but this is compensated
for by the fact that the energy density is underestimated because a
smaller fraction of the total energy is emitted in the radio waveband
and thus included in the integral over source luminosity. As a result,
the actual energy density could be substantially higher than the energy
density I have derived, but is unlikely to be substantially less.
(see Fig. 1) lose a substantial fraction of their energy
to inverse Compton radiation. This effect is even more important if
the magnetic field strength is lower than the equipartition estimate.
Lowering the magnetic field strength of a source reduces its
contribution to the magnetic energy density, but this is compensated
for by the fact that the energy density is underestimated because a
smaller fraction of the total energy is emitted in the radio waveband
and thus included in the integral over source luminosity. As a result,
the actual energy density could be substantially higher than the energy
density I have derived, but is unlikely to be substantially less.
 H_0^3, the
real luminosity L
H_0^3, the
real luminosity L  H_0^-2 and the age of the universe
t_0
H_0^-2 and the age of the universe
t_0