>), (6)
For any model, we can then estimate the value of the diffusion coefficient D required. In practice, rather than a fit I simply choose the value of D that gives the correct intercept on the x-axis. This gives D~0.2, and doesn't vary much between the different field models. This isn't true in general - different models with the same D generally have different intercepts, as shown in the figures.
This value for D is quite interesting. If we assume that there is no diffusion and that the inverse Compton losses are responsible for the value of D, then
D = B_IC^2 / (B_IC^2 +
<B^2 sin^2>), (6)
where <B^2 sin^2>
refers to the expectation value of the losses, so that <B^2
sin^2> = (2/3)B_rms^2,
where the factor 2/3 arises from the dependence of losses on pitch
angle, and we average over pitch angle. For D=0.2, we get
B_rms=
6 B_IC, or B_rms =
8.7
. This is very
much less than the equipartition field (Carilli et al. 1991). Either
the equipartition field is very much in error, or some diffusion of
electrons between regions of different field strength is indicated.
This estimate of the field strength does, however, give a good lower limit on the field strength in Cygnus A, as allowing for diffusion must increase the derived field strength.
We may also use this result to constrain the efficiency of electron diffusion in the lobes of Cygnus A. The lobes have magnetic field structures on scales of a few kpc. The time for a relativistic electron to free stream over this distance is short, only 10^4 yr. The age of the lobes is at least two orders of magnitude larger than this (Carilli et al. 1991). Thus, if the electrons could diffuse through the lobes at speeds ~c, the diffusion coefficient D would be close to unity and the spectral shape and the colour-colour plot would look rather different. The low value of D (in this context) then indicates that electron streaming motions are strongly inhibited, probably by scattering as in the JP model.
The mean free path (or time between scatterings) can be estimated. If
the field has structure on a scale d and the mean free path is
, then a value of
D~0.1 implies that most of the losses are in the local field,
so that the electron manages to diffuse a distance d in the
ageing time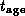 
. The scattering time is /c, so the distance travelled
is
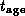d = (c / )
= (c 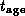). (7)
The age of Cygnus A is 6x10^6 yr in the equipartition case with
B=50 (Carilli et al. 1991) and scales as ~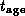
B^-3/2, so taking the typical age of the lobes to be half this, the
mean free path has to be
10 (d/3
kpc)^2 (B/50)^3/2 pc. (8)
The scattering mean free path could well be very much lower than this,
if the field strength were lower as in a self-consistent model, where
B~17
(Carilli et al. 1991), or if there were magnetic field structure on
smaller scales.
While this calculation has been performed for the simple models parameterized by the diffusive efficiency D, similar conclusions are reached if realistic diffusion models such as those in Section 6 are used - the models in which the electrons can stream easily between regions of different field strength do not give a good description of the data.
On to:
Up to: ___________________________________ Peter Tribble, peter.tribble@gmail.com