 ,t) = N_0 E^-
,t) = N_0 E^- [1
-
[1
- 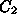 Et (
Et (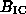 ^2+B^2 sin^2
^2+B^2 sin^2 )]^(
)]^( -2)
(1)
-2)
(1) changes
to (Pacholczyk 1970)
changes
to (Pacholczyk 1970)
N(E, ,t) = N_0 E^-
,t) = N_0 E^- [1
-
[1
- 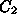 Et (
Et (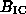 ^2+B^2 sin^2
^2+B^2 sin^2 )]^(
)]^( -2)
(1)
-2)
(1)
where  is the pitch
angle,
is the pitch
angle, 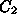 a constant and
a constant and 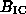 = 3.18(1+z)^2
= 3.18(1+z)^2 is the
equivalent magnetic field strength of the microwave background. In the
JP model the pitch angles are continually randomized and the above
expression is changed by the replacement sin^2
is the
equivalent magnetic field strength of the microwave background. In the
JP model the pitch angles are continually randomized and the above
expression is changed by the replacement sin^2 ->
<sin^2
->
<sin^2 > = 2/3. The
exponent
> = 2/3. The
exponent  is related to
the radio spectral index n by
is related to
the radio spectral index n by  =
2n+1. The depletion of high energy electrons is seen as a fall
in the high frequency radio emission below the extrapolation of the low
frequency emission.
=
2n+1. The depletion of high energy electrons is seen as a fall
in the high frequency radio emission below the extrapolation of the low
frequency emission.
Electron energy losses are highest in the strong field regions, so the spectrum of the radio emission from those regions steepens most rapidly. Thus at high frequencies the emission is biased towards regions of low field strength. There is a difference between the KP and JP models, as in the former the emission from regions where the magnetic field is perpendicular to the line of sight fades faster.
The total emission is given by
I( ,t) = C
,t) = C  N(E,t) F(x) dE, (2)
N(E,t) F(x) dE, (2)
where x =  /
/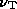 , with
, with
F(x) = x _x^
_x^ K_5/3(z) dz, (3)
K_5/3(z) dz, (3)
and
 _T =
c_1 B
_T =
c_1 B 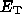 ^2 sin
^2 sin  , (4)
, (4)
where the energy 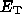 is defined by
is defined by
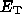 = 1/[
= 1/[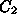 t
(
t
(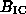 ^2+B^2 sin ^2
^2+B^2 sin ^2 )]. (5)
)]. (5)
The initial radio spectrum is a power law I~ ^-n. The
total aged spectrum can be characterized by a function A(
^-n. The
total aged spectrum can be characterized by a function A( ,x), which
simply multiplies the initial spectrum,
,x), which
simply multiplies the initial spectrum,
I( ,t) = A(
,t) = A( ,x)
I(
,x)
I( ,0). (6)
,0). (6)
Here A is a fixed function, so that the shape of the spectrum
is the same at all times everywhere, and only the single parameter
x is a function of position, while  is a constant
for any source (assuming no reaccelaration) but can vary between
sources.
is a constant
for any source (assuming no reaccelaration) but can vary between
sources.
To get the total spectrum for a source, one must then sum over the
entire volume, or equivalently sum over all angles and field strengths.
The initial intensity I( ,0)
,0)  (B
sin
(B
sin  )^n+1
determines the relative contributions to the spectrum from different
points.
)^n+1
determines the relative contributions to the spectrum from different
points.
I assume that the magnetic field can be described by a Gaussian random field. Then the angles are distributed isotropically and the field is drawn from a Maxwellian distribution. In Fig. 1 I show the resulting spectra for both KP and JP models compared with the spectra that would result if the field strength were uniform. Especially in the JP case, the spectra are flatter at high frequencies than in the constant field-strength case. The spectrum initially falls below the constant field-strength case but remains fairly flat. The initial fall is due to increased losses from the regions of highest field strength; the remaining emission then decays more slowly.
![[Figure 1]](fig1.gif)
Fig 1. Aged spectra as a function of frequency for the KP model (top) and JP model (bottom). The aged spectrum assuming a random field strength is shown as a solid line, and that from a constant field shown as a dotted line for comparison.
The reason for the smoothing out of the sharp spectral decline is quite
simple. The resultant spectrum is the superposition of many spectra all
with different break frequencies 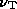 . In
the standard KP model, the break frequency depends on pitch angle. In
the models in this paper, the break frequency depends in addition on
the local field strength. The resultant smearing out of the sharp
spectral break depends simply on the presence of a range of field
strength and is not specific to a Gaussian field.
. In
the standard KP model, the break frequency depends on pitch angle. In
the models in this paper, the break frequency depends in addition on
the local field strength. The resultant smearing out of the sharp
spectral break depends simply on the presence of a range of field
strength and is not specific to a Gaussian field.
In Fig. 2 I show how the spectral index varies with time. The spectral
index is that between the two frequencies  _1 and
_1 and  _2,
plotted against
_2,
plotted against  (
( _1/
_1/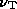 ) which is proportional to time. This figure is then
directly comparable to Figs. 2 and 3 of Myers & Spangler (1985),
although I have used consistent definitions of
) which is proportional to time. This figure is then
directly comparable to Figs. 2 and 3 of Myers & Spangler (1985),
although I have used consistent definitions of 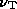 in the KP and JP cases (Leahy, Muxlow & Stephens
1989). When plotted in this way, considerable differences between the
models are apparent. When the amount of spectral aging is small, the
two point spectral index tends to overestimate the age slightly. When
the spectral aging is large, the two point spectral index substantially
underestimates the age.
in the KP and JP cases (Leahy, Muxlow & Stephens
1989). When plotted in this way, considerable differences between the
models are apparent. When the amount of spectral aging is small, the
two point spectral index tends to overestimate the age slightly. When
the spectral aging is large, the two point spectral index substantially
underestimates the age.
![[Figure 2]](fig2.gif)
Fig 2. Two frequency spectral index as a function of time. Solid lines are KP models, while JP models are dashed lines. The higher two curves are for the unmodified (uniform field strength) models, while the lower curves are for the random field strength case.