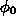 to a field of
strength B_0 and travelling at speed v then
to a field of
strength B_0 and travelling at speed v then
As an electron travels along a field line, any change of magnetic field
strength causes the pitch angle of the electron to change so as to keep
the magnetic flux linked by the orbit constant. If the electron is
initially at pitch angle 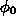 to a field of
strength B_0 and travelling at speed v then
to a field of
strength B_0 and travelling at speed v then
B / sin^2 = B_0 /
sin^2
= B_0 /
sin^2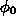 . (7)
. (7)
The velocity components perpendicular and parallel to the field are
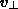 = v sin
= v sin 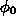
 (B/B_0);
(B/B_0);
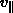 = v
= v  (1-B
sin^2
(1-B
sin^2 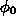 /B_0), (8)
/B_0), (8)
respectively.
The losses are proportional to B^2 sin^2 . This needs to
be averaged along the orbit, along which B/ sin^2
. This needs to
be averaged along the orbit, along which B/ sin^2 is a
constant, so that the average losses are proportional to
is a
constant, so that the average losses are proportional to
 B^3
W(s) ds. (9)
B^3
W(s) ds. (9)
The integral is over all the path s that the electron can
reach, with B<B_max where B_max =
B_0/sin^2 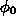 is the maximum
field strength into which the electron can travel (it is mirrored out
of stronger fields) and W(s) is proportional to the length of
time the electron spends in a region ds of a particular field
strength. I will assume that the probability of a field strength
B is the same for all electrons, and the time spent in a
region of field strength B is inversely proportional to the
velocity
is the maximum
field strength into which the electron can travel (it is mirrored out
of stronger fields) and W(s) is proportional to the length of
time the electron spends in a region ds of a particular field
strength. I will assume that the probability of a field strength
B is the same for all electrons, and the time spent in a
region of field strength B is inversely proportional to the
velocity 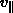 corresponding to that field
strength. The average losses for an electron are then
corresponding to that field
strength. The average losses for an electron are then
<B^2 sin^2 >_orbits =
>_orbits =
 _0^B_max B^3 P(B) (1-B/B_max)^-1/2 dB
(sin^2
_0^B_max B^3 P(B) (1-B/B_max)^-1/2 dB
(sin^2 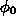 / B_0) --------------------------------------------
/ B_0) --------------------------------------------
 _0^B_max P(B) (1-B/B_max)^-1/2 dB
_0^B_max P(B) (1-B/B_max)^-1/2 dB
= L(B_0/
sin^2 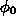 ). (10)
). (10)
![[Figure 3]](fig3.gif)
Fig 3. The mean losses of an electron as a function of the
initial value of B_0/sin^2 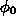 .
.
The mean losses are shown as a function of B_0/sin^2 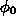 in Fig. 3. Note that average electrons have
the largest losses. An electron with a large B_0/sin^2
in Fig. 3. Note that average electrons have
the largest losses. An electron with a large B_0/sin^2 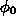 spends the vast majority of its time in
regions of low field strength travelling nearly parallel to the field,
and consequently has low average losses. The mean losses in this case
are only about 80% of what they were before.
spends the vast majority of its time in
regions of low field strength travelling nearly parallel to the field,
and consequently has low average losses. The mean losses in this case
are only about 80% of what they were before.
The electron energy spectrum in this case becomes
N(E, ,t) = N_0 E^-
,t) = N_0 E^- (1 -
(1 - 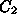 Et [
Et [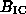 ^2+L(B/ sin^2
^2+L(B/ sin^2 )])^(
)])^( -2).
(11)
-2).
(11)
![[Figure 4]](fig4.gif)
Fig 4. The synchrotron spectrum from electrons in a random magnetic field with no pitch angle scattering (solid line), with the standard KP model spectrum as a dotted line for comparison.
The total spectrum is again obtained by using equation (11) in equation (2) and averaging over all angles and field strengths. The result is shown in Fig. 4. In this case, spectral aging is systematically slower than in the standard KP model.