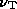
 B
varies. This is equivalent to a case where the electrons sample not
only all pitch angles but all field strengths. Models with both
synchrotron and inverse Compton losses can be described by equation
(12) if we make the identification
B
varies. This is equivalent to a case where the electrons sample not
only all pitch angles but all field strengths. Models with both
synchrotron and inverse Compton losses can be described by equation
(12) if we make the identificationIf diffusion between regions of different field strengths is only partial then we might consider a model in which the energy losses of an electron are proportional to
<B^2>_electron = D <B^2> + (1-D) B^2, (12)
which is a combination of the local field B and the average field seen throughout the electron's lifetime. If D=0 then we recover the spectrum described in Section 2, whereas for larger D then the spectrum declines more sharply at high frequencies. Strictly, D should be a function of energy as it depends on both the diffusion time and the energy loss time.
Exactly the same formalism can be applied to a source with a weak
magnetic field, so that energy losses are dominated by inverse Compton
scattering off the microwave background [this might also be true for
radio halos in galaxy clusters (Kim, Tribble & Kronberg 1991), or
for sources at high redshift where the energy density of the microwave
background is much greater]. In the extreme case the electron energy
spectrum is the same everywhere. The radio spectrum differs from place
to place because the break frequency 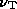
 B
varies. This is equivalent to a case where the electrons sample not
only all pitch angles but all field strengths. Models with both
synchrotron and inverse Compton losses can be described by equation
(12) if we make the identification
B
varies. This is equivalent to a case where the electrons sample not
only all pitch angles but all field strengths. Models with both
synchrotron and inverse Compton losses can be described by equation
(12) if we make the identification
D = 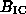 ^2 / (
^2 / (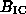 ^2 + <B^2>). (13)
^2 + <B^2>). (13)
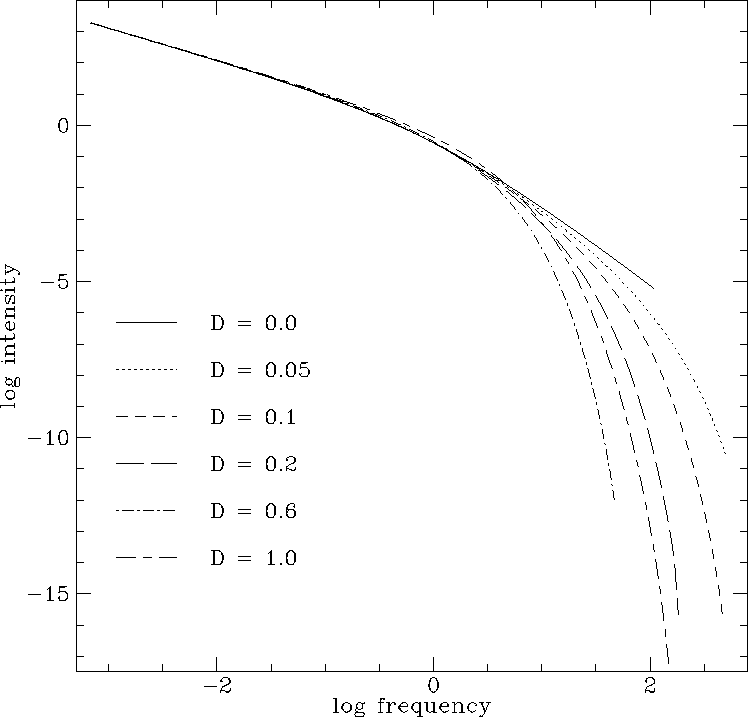
Fig 5. The synchrotron spectrum from electrons in a random magnetic field with pitch angle scattering for various values of the diffusion coefficient D.
I have calculated the spectra for various values of D and show
the results in Fig. 5. For small values of D the spectra do
not show a sharp break, but this break is apparent for
D~>0.2. For D=1 a sharp break is seen, although
not quite as sharp as in the standard JP model. Interestingly, for
large values of D the spectrum steepens more rapidly than for
D=1. This is because a little variation in the energy losses
compensates for the factor B in the numerator of 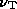 , so that
, so that 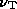 varies very little.
varies very little.
If we just consider the effect of inverse Compton losses, then powerful
sources with very high field strengths should have radio spectra
similar to the KP model. This is indeed the case for Cygnus A (Carilli
et al. 1991), where the averaging is mainly along the line of sight as
the observations have fairly good resolution. Other sources have
equipartition field strengths that are at most a few 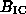 (eg. 3C234, Alexander 1987), and these sources would be
expected to have spectra that are much closer to the JP model. Careful
fitting of high frequency spectra could be used to check the
reliability of magnetic field strength estimates in radio sources.
(eg. 3C234, Alexander 1987), and these sources would be
expected to have spectra that are much closer to the JP model. Careful
fitting of high frequency spectra could be used to check the
reliability of magnetic field strength estimates in radio sources.