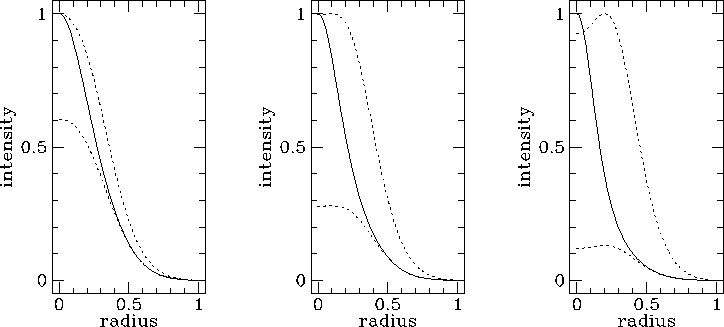
Fig 5. Intensity profiles for three hotspots with different 
_eff
= 0.1, 0.25, 0.4, from left. The hotspots are intrinsically Gaussian
with the emission 50% more extended than the velocity. The approaching
hotspot is shown as a solid line, the receding hotspot as the lower
dashed line. The upper dashed line is the receding hotspot amplified so
that its shape can be compared with that of the approaching hotspot.
In fact, beaming alone can provide a trivial explanation of the compactness asymmetry. Describing the hotspot as a monolithic entity moving at a single speed is obviously incorrect. In reality, there will be some velocity gradient between the core of the hotspot and the stationary lobe.
To show this I consider a simple model with a monotonic velocity
gradient from the central value of _0 to zero for
the lobes which are assumed to be at rest. The important feature here
is that for the approaching hotspot the centre is preferentially
enhanced by beaming relative to the slower hotspot material, whereas
for the receding hotspot the flux from the centre is preferentially
reduced. The peakiness of the approaching hotspot is increased whereas
the receding hotspot is flattened. In fact, it is possible to create an
inverted receding hotspot with the observed flux decreasing toward the
centre.
I take the emission I and the velocity to fall as
Gaussians,
I(r) = I_0 exp(-r^2/r_I^2)
(r) = _0
exp(-r^2/r_^2).
(20)
The results depend quite strongly on the ratio R=r_I/r_
of the sizes of these two distributions. The hotspot is lit up where
the beam hits the working surface, so the emissivity process is
connected with deceleration. This leads us to expect that R should be
not too different from and possibly somewhat greater than unity. Some
examples of hotspot profiles are shown in Fig. 5. I define the
compactness ratio as the ratio of the full widths at half maximum of
the approaching and receding hotspots. This is shown for different
values of R and _eff=_0
in Fig. 6.
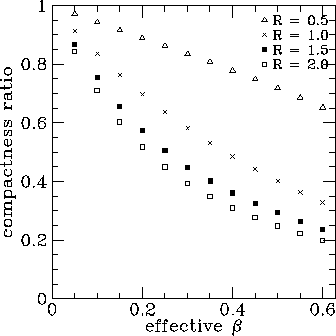
Fig 6. The compactness ratio as a function of _eff for
Gaussian hotspots of different emission to velocity size ratios R.
An alternative model is to have material flowing through the hotspot at
a velocity _0 and an
associated backflow at velocity _1. Material is
continually moving through the hotspot so that the pattern speed of the
hotspot can be very much less than _0. This has the
same qualitative features as the previous model with the exception that
the outer emission might be brighter in the receding half of the
source, boosted by the backflow approaching the observer.
The central value of _0 can be larger
than either the value required to explain the hotspot luminosity and
spectral index asymmetry or the upper limit on the advance speed from
the lobe separation asymmetry (Longair & Riley 1979). This is
because the hotspot flux and spectral index asymmetry depend on the
emission weighted , and the
separation asymmetry measures the pattern speed of the hotspot, which
might both be substantially less than the flow speed of the emitting
material.
If the hotspots are substantially beamed then they are also enfeebled
by several powers of 
=(1-^2)^-1/2. This
won't affect the asymmetry as both sides are equally affected. If,
however, a secondary hotspot is present (Laing 1981; Valtaoja 1984;
Lonsdale & Barthel 1984, 1986) then the relative properties of the
primary and secondary hotspots will be affected. I assume that the
primary jet loses a substantial fraction of its momentum at the primary
hotspot, so that the reflected jet feeding the secondary hotspot has
<<1 and
Doppler boosting is negligible for the secondary. Therefore the two
secondaries (assuming there to be one on each side) will appear rather
similar. The approaching primary will be more compact, and the receding
primary will be diffuse. If the approaching primary and secondary are
of similar luminosity, then the receding primary will be much fainter
than its corresponding secondary. Thus the receding side might only
appear to contain one hotspot which is actually the secondary (see
Lonsdale 1989). This picture is consistent with the hotspots of
Cygnus~A (Carilli, Dreher & Perley 1989) where the primary hotspot
on the counterjet side is rather weak compared to the secondary.
In Section 4 I showed how a spectral index asymmetry can be given by Doppler boosting of the hotspots. Exactly the same argument predicts a spectral index asymmetry for the hotspots alone. As the emitting plasma in the hotspots is decelerated, the relativistic electrons are losing energy and the emitted spectrum is steepening, giving a spectral index gradient across the hotspot. The approaching hotspot is dominated by the centre where the spectrum is flattest, so that if the hotspots are unresolved the total spectrum of the approaching hotspot will be flatter than that of the receding hotspot.