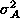Model Details

The images in this paper have a power spectrum for the vector potential A of the form

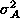(k) = k^2 exp(-k^2/k_0^2). (1)

The magnetic field power spectrum is calculated as Btilde = ik Ã. This form is chosen because the incompressible nature of the field requires 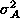(k) ~ k^2 at small k (see Batchelor 1953).

The small size of the computational volume makes it difficult to fit in a power-law power spectrum between upper and lower cutoffs, so this is not attempted here and the effects of various different power spectra will be studied in a subsequent paper. The models in this paper are characterized by a single scale which I have set to 4 pixels or one sixteenth of the size of the computational box. Changing this scale makes no difference to the effects discussed in this paper, which concentrate solely on the effects of ageing on the evolution of a given radio image.

Once the magnetic field has been set up in the box, a population of relativistic electrons with a power-law energy spectrum is added. I assume the particle number density and initial energy spectrum to be independent of position. This means that both the total energy density and the ratio of particle to field energy densities must vary throughout the volume. Equipartition does not hold locally, even if it is true on average. Although assuming that the particle pressure is independent of position is almost certainly incorrect, a proper treatment must take full account of dynamical processes. While a limitation, many numerical simulations (Clarke et al. 1989; Matthews & Scheuer 1990a,b) and the instability analyses assume that the particle pressure dominates, so that total pressure variations are small. While some models of radio sources with dynamically important magnetic fields have been run, they do not appear to give a good description of radio lobes (Norman, Clarke & Burns 1987).

If the low-frequency radio spectrum has spectral index (where I() ^{-} - the images presented here are for = 0.5) then the emission intensity I depends on the local field strength B and angle between the field direction and the line of sight as

I (Bsin)^{+1}. (2)

I have already considered such images in a different context (Tribble 1991), where I showed that spatial fluctuations in radio intensity allowed one to deduce (or limit) the scale length of the magnetic field fluctuations. The polarization and power spectra of the synchrotron emission from a turbulent magnetic field has also been studied by Eilek (1989a,b).

At higher frequencies the emission falls due to energy losses of the relativistic electrons. The theory has been given by Pacholczyk (1970) and I repeat the salient points here. The initial energy spectrum N(E) = N_0 E^{-} allowing for inverse Compton and synchrotron losses at each point evolves to become

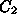N(E,,t) = N_0 E^{-} [1 - Et (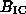^2+B^2sin^2)]^{-2} (3)

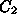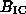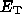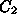where is a constant, is the electron pitch angle, and the equivalent field strength of the microwave background. I assume that the pitch angles are rapidly isotropized by scattering (Jaffe & Perola 1973), so that <sin^2>=2/3. The energy spectrum (3) can be written in terms of a break energy = 1/[ t 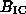^2 + B^2sin^2)],

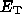N(E,t) = N_0 E^{-} [1 - E/]^{-2}. (4)

The emitted intensity is given by

I(,t) ~ N(E,t)F(x) dE, (5)

where x = / 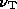and 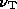= c_1 B 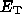^2 sin with c_1 a constant. For the polarization, F(x) is replaced by G(x) where

F(x) = x_x^ K_5/3(z) dz, G(x) = xK_2/3(x). (6)

The integrals over F and G are calculated in advance and stored as a lookup table.

The emission from any point in the volume can thus be characterized by a single function of the local break frequency 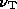, which depends on the losses which determine the break energy 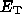and the local field strength. The radio emission from a point has a break frequency

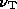
B sin / [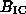^2 + (2/3)B^2]^2, (7)

where the equivalent field strength of the microwave background is 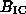= 3.18 (1+z)^2.

As discussed by Tribble (1993), diffusion can be treated in the same way as inverse Compton losses. We could write (neglecting inverse Compton losses for the moment)

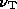
B sin / [D(2/3)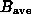^2 + (1-D)(2/3)B^2]^2, (8)

where the relativistic electron has spent a fraction D of its lifetime losing energy at a rate determined by the average rms field strength 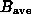of the regions the electron has been in, and has spent the most recent fraction (1-D) of its life losing energy at a rate determined by the field at its current location. I assume that 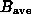is equal to the rms field strength averaged over the entire volume. While this is a very simplistic way of treating diffusion, with D a ``diffusion efficiency,'' there is a clear equivalence between Eqs. (7) and (8). It can be seen that inverse Compton models with a high field strength correspond to low diffusion. In general, it is the ratio of local and global losses that is important. The local losses are associated with the field strength where the electron is currently radiating, while the global losses are due to inverse Compton scattering, diffusion, or a combination of the two effects.

For the static models considered here a series of images of different frequency is equivalent to the same image at different times. Each image in the series is constructed by choosing a frequency , then for each point in the model volume finding the emission at corresponding to the value of 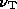at that point. The emission from all the grid points along each line of sight is added to give the intensity of the image. A similar procedure is followed to make images in polarization, with the added complication that the polarized intensity is a vector quantity.

In this paper I present three simulations, with different field strengths. The three simulations are for weak, intermediate, and strong fields, in which the rms field strength is 0.3, 1, and 4 relative to the microwave background equivalent respectively. These are equivalent to diffusion models with D = 0.943, 0.6, and 0.0857 (Tribble 1993). These simulations cover a range of radio sources. For example, radio halos in galaxy clusters have weak fields ~1 (Kim et al. 1990), large radio sources have magnetic fields ~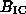 (e.g. 3C234, Alexander 1987), and powerful sources like Cygnus A have much stronger fields. It is less easy to relate the different diffusion models to particular sources, as the effectiveness of electron diffusion in radio sources is unknown, but the simulations presented here cover the two extreme possibilities and an intermediate case. Note that the shape of the spectrum is different for different field strengths or diffusion efficiencies (Tribble 1993), and the break frequency 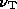is also different. However, I define a mean break frequency for each simulation,

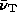= 0.5 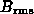/ [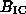^2 + (2/3)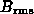^2]^2, (9)

with an analogous definition if we wish to work in terms of diffusion. The frequency in the models is in terms of this 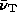, so that the break frequency is the same for all models. This allows the different models to be compared without having to worry about the different frequency normalizations.

On to:

• Section 3

• Index