Polarization

The following comments only apply to emission from a volume in which the field is random and isotropic. The observed polarization from powerful edge brightened radio sources implies that the field structure is highly sheared (as in the models of Laing 1980). In a sheared field configuration, the polarization properties are dominated by the shear, so that the source physics is more important.

The polarization behaviour is dependent on the field strength and diffusion coefficient. I will describe the three cases separately.

When the field strength is low, or the diffusion strong, the polarization angle usually changes very little with frequency, while the fractional polarization grows slowly. The reason for the relatively small change in the polarization angle is that the polarization is determined by the brightest points along the line of sight, and the same volume elements dominate the emission of a line of sight at all frequencies. They do fade at slightly different rates, so that as the frequency is increased fewer points along the line of sight contribute to the observed polarization vector. Ultimately, the polarization will be determined by the point along the line of sight where the field is strongest, as that will be the last point to fade. Because this point was also strong at low frequencies, the angles at low and high frequencies are correlated.

For intermediate fields and diffusion coefficients, many points have almost constant polarization as before. However, there are some points which show larger variations. These points also have complex behaviour in fractional polarization. This behaviour is due to several (usually two in these small simulations) regions of emission along the line of sight interfering with each other and fading at different rates. In most cases, most of the variation is at low frequencies / < 1. Because regions of different field strength fade roughly at the same rate, the emission at high frequency has contributions from all along the line of sight and the overall increase in polarization is rather small.

In the strong field case, there are large rapid variations in polarization angle at low frequency. This again is interference between different components along the line of sight fading at different rates. The existence of fluctuations in the angle and fractional polarization are correlated. The angle rapidly becomes uncorrelated with its initial value as the points dominating the emission at low frequencies fade and are replaced by other points with different polarization angles.

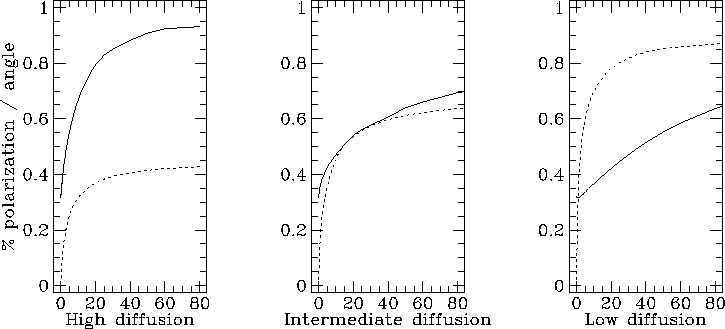
Fig. 9 The rms fractional polarization (solid line) and the rms angle (in radians) rotated from the lowest frequency image (dotted line) as a function of frequency for the three simulations.

These trends are shown in Fig. 9, where I show the rms fractional polarization of the image as a function of frequency, along with the rms angle rotated from the initial angle. As the field strength is increased, or diffusion made less efficient, the polarization angle changes more with frequency.

What is notable about the polarization behaviour is that much of the change occurs at low frequency. At high frequencies the polarization can become large, and usually changes very little, as the polarization is then dominated by a single region along the line of sight.

On to:

• Section 6

• Index