 .
These three quantities are related by
.
These three quantities are related by
I assume that there is energy equipartition between fields and
radiating particles in the source (although see Leahy 1989). I further
assume that all of the energy E in particles (there is also an
energy E in the field) is radiated to give a source luminosity
L for a lifetime  .
These three quantities are related by
.
These three quantities are related by
L = E /  . (2)
. (2)
If the radio luminosity function (the number of sources per unit volume
per unit luminosity interval) is denoted by  (L), then the birthrate function
is
(L), then the birthrate function
is
d  (L) dt =
(L) dt =  (L) /
(L) /  (L) = L
(L) = L  (L) / E. (3)
(L) / E. (3)
The rate of energy creation in radio sources is the source birthrate multiplied by the energy of each source, or
d^2 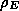 / dL dt =
E d
/ dL dt =
E d (L) /
dt = L
(L) /
dt = L (L), (4)
(L), (4)
where 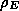 is the energy density in
magnetic fields. If the universe were not expanding, this would also
equal the energy density in radiation, but the radiation energy density
is decreased because the radio waves are redshifted away. The rhs of
equation (4) is equal (to within a factor ln 10) to the logarithmic
radio luminosity function.
is the energy density in
magnetic fields. If the universe were not expanding, this would also
equal the energy density in radiation, but the radiation energy density
is decreased because the radio waves are redshifted away. The rhs of
equation (4) is equal (to within a factor ln 10) to the logarithmic
radio luminosity function.
To calculate the total energy input into radio sources we must then integrate equation (4) over both luminosity and time, so that
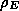 =
= 
 L
L  (L) dt dL =
(L) dt dL = 
 (1/ln 10}(d N(L) / d log
L) dt dL. (5)
(1/ln 10}(d N(L) / d log
L) dt dL. (5)
The radio luminosity function at 2.7 GHz has been given by Dunlop & Peacock (1990). For the steep spectrum sources, which are those of interest here, they gave a luminosity function of the form
dN(L) / d log L = 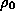 /
[(L/
/
[(L/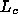 )^
)^ +(L/
+(L/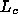 )^
)^ ] (6)
] (6)
where
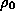 = 10^-6.91 Mpc^-3,
= 10^-6.91 Mpc^-3,
 = 0.69,
= 0.69,
 = 2.17, (7)
= 2.17, (7)
and
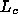 (z) = 10^24.89 10^(1.26z-0.26z^2) W Hz^-1
sr^-1. (8)
(z) = 10^24.89 10^(1.26z-0.26z^2) W Hz^-1
sr^-1. (8)
We then get
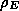 =
= 
 (1 / ln 10)
(1 / ln 10) 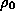 /
[(L/
/
[(L/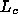 )^
)^ +(L/
+(L/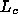 )^
)^ ] dt dL.
(9)
] dt dL.
(9)
In a simple  = 1
cosmology, the time t is related to the age of the universe
t_0 and redshift z as
= 1
cosmology, the time t is related to the age of the universe
t_0 and redshift z as
t = t_0/(1+z)^3/2, (10)
so that, integrating over all sources more luminous than 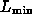 and up to a maximum redshift
and up to a maximum redshift 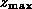 ,
,
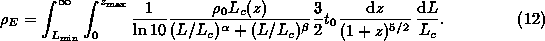
With the substitution y = L/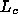 , this is
, this is
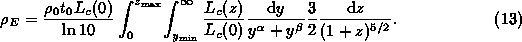
Strictly, 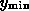 is a function of z
(because it depends on
is a function of z
(because it depends on 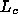 ). However, very
little error in evaluating the integral over y in Eq. (12) is
made if the lower limit is replaced by
). However, very
little error in evaluating the integral over y in Eq. (12) is
made if the lower limit is replaced by 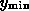 = 0, so I will make this assumption, which allows the
integrals over y and z to be separated into two
factors,
= 0, so I will make this assumption, which allows the
integrals over y and z to be separated into two
factors,
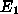 (
(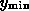 ) =
) =  _
_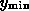 ^
^ d
y / (y^
d
y / (y^ +y^
+y^ ) (13)
) (13)
and
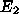 (
(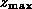 ) =
) =  _0^
_0^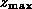 [
[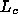 (z) /
(z) / 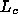 (0)]
(3/2)d z/(1+z)^5/2. (14)
(0)]
(3/2)d z/(1+z)^5/2. (14)
I show the values of the integrals in Figs 1 and 2. As can be seen
quite clearly, the choice of 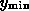 and
and 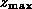 makes very little difference to the final result, so I
take limiting values which are
makes very little difference to the final result, so I
take limiting values which are 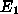 = 3.47 and
= 3.47 and
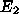 = 7.87.
= 7.87.
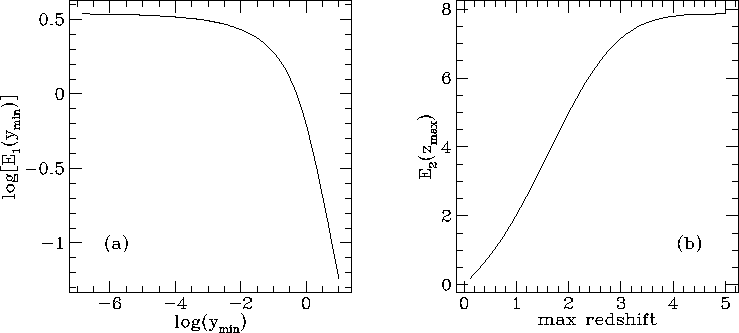
Fig. 1. The values of the integrals 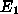 (
(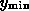 ) [(a), left] and
) [(a), left] and 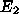 (
(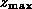 ) [(b),
right].
) [(b),
right].
The accumulated energy density is then
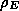 = 11.86
= 11.86 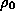 t_0
t_0 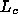 (0). (15)
(0). (15)
We aren't quite yet finished, as 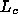 is in W Hz^-1 sr^-1
at 2.7 GHz, and we require the bolometric luminosity, which involves
integrating over frequency
is in W Hz^-1 sr^-1
at 2.7 GHz, and we require the bolometric luminosity, which involves
integrating over frequency  and solid
angle. If the radio spectrum is a power law of spectral index
n (so that I(
and solid
angle. If the radio spectrum is a power law of spectral index
n (so that I( )
) 
 ^-n), then
^-n), then
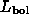 = 4
= 4
 I(
I( ) d
) d = 4
= 4
 I(
I( )
) (
( /
/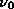 )^-n d
)^-n d /
/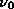 .
(16)
.
(16)
Integrating over a range  _min to
_min to
 _max gives
_max gives
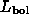 = 4
= 4
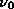 I(
I(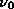 ) [(
) [( _max/
_max/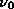 )^(1-n) -
(
)^(1-n) -
( _min/
_min/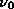 )^(1-n)] /(1-n). (17)
)^(1-n)] /(1-n). (17)
For the sources in their sample Dunlop & Peacock find n =
0.85, which has the advantage that the total luminosity is not very
sensitive to the cutoff frequencies chosen. With  _max a few times
_max a few times 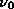 and
and  _min <<
_min <<
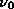 , we get
, we get
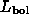
 4
4
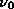 I(
I(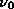 )/(1-n). (18)
)/(1-n). (18)
The bolometric luminosity corresponding to 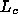 (0) is
(0) is
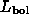 = 4
= 4
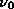 10^24.89/(1-n) =
1.75x10^36 W. (19)
10^24.89/(1-n) =
1.75x10^36 W. (19)
The total energy density (equation 15) is then
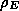 = 1.07x10^48 J Mpc^-3. (20)
= 1.07x10^48 J Mpc^-3. (20)