0.11} (L_x / 10^44
erg/s)^{-2.170.15}
(10^44 erg/s)^-1 Mpc^-3, (21)
dN / dL_x = 10^{-6.650.11} (L_x / 10^44
erg/s)^{-2.170.15}
(10^44 erg/s)^-1 Mpc^-3, (21)
and the temperature function is
dN / dT = 10^{-3.960.26} T^{-4.930.37} Mpc^-3 keV^-1. (22)
The integrated space densities of clusters with luminosities exceeding
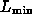or temperatures exceeding 
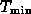are
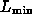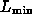N(>) = {10^{-6.650.11} / 1.170.15} ( / 10^44 erg/s)^{-1.170.15} Mpc^{-3}, (23)
and
N(>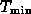) = {10^{-3.960.26} / 3.930.37} 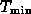^{-3.930.37} Mpc^{-3}. (24)
In both cases, integrating down to fairly poor clusters (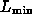 ~ a few x10^43 erg/s or 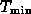~2 keV) gives a total space density of 10^-6
per cubic Mpc. A similar space density is obtained by simply taking
Abell's (1958) statistical sample of galaxy clusters. Bahcall (1979)
gives the space density of Abell R=1 clusters to be 1.2x10^-6
per cubic Mpc. The space density of rich clusters of galaxies is
therefore about 10^-6 per cubic Mpc, and I will use this value in the
following discussion.
As emphasized in Section 2, most of the
magnetic remnants will be incorporated in clusters. With a cluster
space density of 10^-6 per cubic Mpc and a magnetic energy density of
10^48 J per cubic Mpc, this gives about 10^54 J for the magnetic energy
in a rich cluster. The important point to note is that this energy is
more than adequate to give a 1
field in a
galaxy cluster. We could consider two possible models for the
intracluster magnetic field. A uniform 1 field in a
sphere of radius 1 Mpc gives a total energy of almost 5x10^53
J, while if the magnetic field declines with radius as B^2 ~
[1.0 + (r/r_0)^2]^{-3/2} from a central value of 1 with r_0 = 250
kpc then the magnetic energy out to large radii is still less than
10^53 J.
The figure of 10^54 J per cluster is an average value. In particular, it is an average over clusters of a variety of richnesses. Richer clusters are expected to accumulate more magnetic energy, simply because they are more massive and thus will have accumulated more magnetic remnants. Clusters as rich as the Coma cluster would be expected to have accumulated rather more than the average 10^54 J of magnetic energy.