Sheared field models

Laing (1980) presented models of radio sources in which the magnetic field has been sheared or compressed, so that the field is no longer isotropic but is confined to a plane. In general, we would expect twisting and compression of the random field to result in a field that is locally one- or two-dimensional rather than having a full three-dimensional structure. For example, if the field is compressed or sheared into a plane then there are only two significant components of the field. Models of different dimensionality differ in how much of the volume contains a field of a given strength, given by the probability distribution P(B) of field strength B,

P(B) = [2 / (n/2)^n Gamma(n/2)] B^{n-1} exp(-nB^2/2) (2)

where n is the dimensionality of the field.

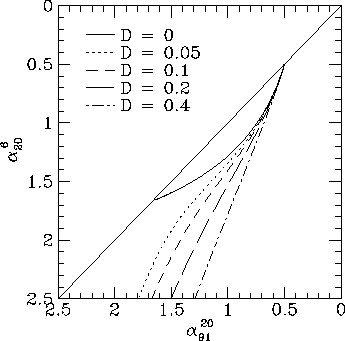
Figure 6. Loci in the colour-colour plane for two-dimensional random field radio spectra, for the set of frequencies (6, 20, 91) cm.

I have simulated synchrotron spectra for the two- and one-dimensional cases, assuming that the averaging is over all angles. This assumes that the source contains planes or tubes of field that are randomly oriented. Fig. 6 shows colour-colour diagrams for a two-dimensional field. I have also considered the case where a two-dimensional field is present in a single plane at various angles to the line of sight. The resulting colour-colour diagram is very similar to the integrated two-dimensional case.

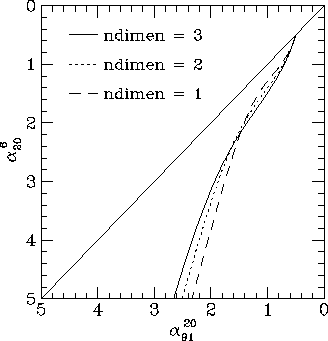
Figure 7. A colour-colour diagram with D=0.1 for a random magnetic field in one-, two-, and three-dimensions, for the set of frequencies (6, 20, 91) cm.

The colour-colour plots for the different dimensional cases are shown for a diffusion coefficient D=0.1 in Fig. 7. While the colour-colour loci of the various models have the same general shape, changing the dimensionality of the field makes substantial detailed differences to the colour-colour diagram. The parallel section of the colour-colour locus moves closer to the equal spectral index line as the dimensionality of the field decreases. This is attractive, as the colour-colour diagram for Cygnus A shows a parallel section that is close to the diagonal (Katz-Stone et al. 1993).

On to:

Up to: ___________________________________
Peter Tribble, peter.tribble@gmail.com