Other field distributions

The random field models of various dimensionality differ solely in the distribution of field strength. Other field models are possible in which the magnetic field isn't based on a Gaussian random field, so that the probability distribution of field strength could then be considered a free parameter.

I have considered three simple distributions. They are an increasing triangle, a rectangular distribution, and a decreasing triangle, denoted as models 1, 2, and 3 respectively. All the models are normalized to have rms field strength equal to unity.

The probability distributions of the field strength B are then

  1. P(B) = B for B<sqrt2
  2. P(B) = 1/sqrt3 for B<sqrt3
  3. P(B) =(sqrt6-B)/3 for B<sqrt6
As we progress from model 1 to 3, the field distribution changes from a generally high field with occasional regions of low field, to a model with rare regions of high field on a low field background. The colour-colour plot changes substantially. The general shape of the colour-colour loci is similar to the random field models, with the differences between the different field distribution being more pronounced in this case due to the larger differences between the magnetic field distributions.

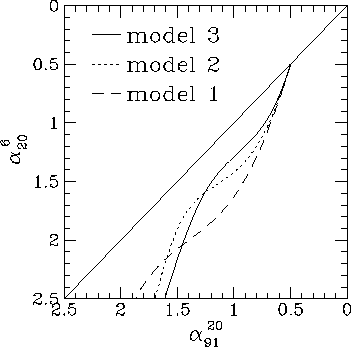
Figure 8. Colour-colour diagrams for the simple field distribution models, for D=0.1, for the set of frequencies (6, 20, 91) cm.

The parallel section of the colour-colour locus moves closer to the diagonal line as the probability distribution is biased toward lower fields. This is also true for the Gaussian field models - the probability distribution (equation 2) of an n-dimensional random field B has a factor B^n-1 which skews the distribution to higher fields in the higher dimensional cases. This dependence of the shape of the colour-colour plot on the magnetic field model is therefore a potentially useful tool for studying the magnetic field distribution in radio sources.

On to:

Up to: ___________________________________
Peter Tribble, peter.tribble@gmail.com